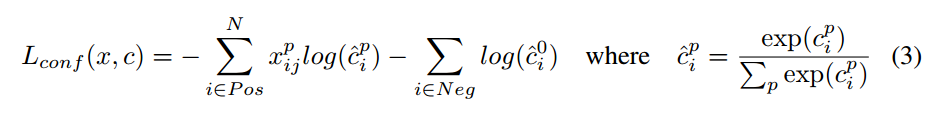前言
目前检测的主流算法分为两种类型:
(1)two-stage方法:如R-CNN系列的算法,其主要思路是先通过启发式方法(selective search)或者CNN网络(Region Proposal Net)产生一系列稀疏的候选框,然后对这些候选框进行分类和回归,其优势是准确度高;
(2)one-stage方法: 如Yolo和SSD,其主要思路是均匀地在图片的不同位置进行密集抽样,抽样时可以采用不同尺度和长宽比,然后利用CNN提取特征后直接进行分类与回归,整个过程只需要一步,所以其优势是速度快,但是均匀的密集采样的一个重要缺点是训练比较困难,这主要是因为正样本与负样本(背景)极其不均衡,导致模型准确度稍低。
SSD,全名Single Shot MultiBox Detector,Single Shot指明了SSD算法属于one-stage方法,MultiBox指明了SSD是多框预测。
Model
- 网络模型如上图,前面是一个VGG层用于特征提取,与VGG的区别是把FC6和FC6换成了卷积层,SSD在后面又加了8个卷积层。
- 最终用于预测的是从这些具有金字塔结构的层中选出的特定层,这些层分别对不同scale和不同aspect ratios的 bounding box进行预测。
- bounding box是 detector/classifier 对 default box 进行回归生成的,而 default box 是由一定规则生成的,这里可以认为 default box 比较像 Faster R-CNN 中的RPN生成的region proposal ,也就是两步检测方案中候选框的作用。
- detector/classifier对这些 default box 进行关于 类别 和 位置的 回归,然后得出一个类别得分和位置坐标偏移量。根据坐标偏移量可以计算出bounding box的位置,根据得分确定此bounding box里的物体类别(每个类别都包含 8732个 bounding box,大部分都是背景 或者说共有 8732个bounding box,每个bounding box 都对一个 C 维的得分,C为类别总数)。
- 最后通过NMS(非最大值抑制)过滤掉背景和得分不是很高的框(这个是为了避免重复预测),得到最终的预测。
YOLO与SSD的主要不同:
SSD是在多个feature map上进行的多尺度(multi-scale)预测(每个feature map预测一种 scale)。而YOLO是只在一个feature map上进行 多尺度预测。
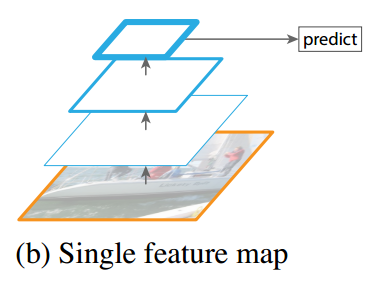
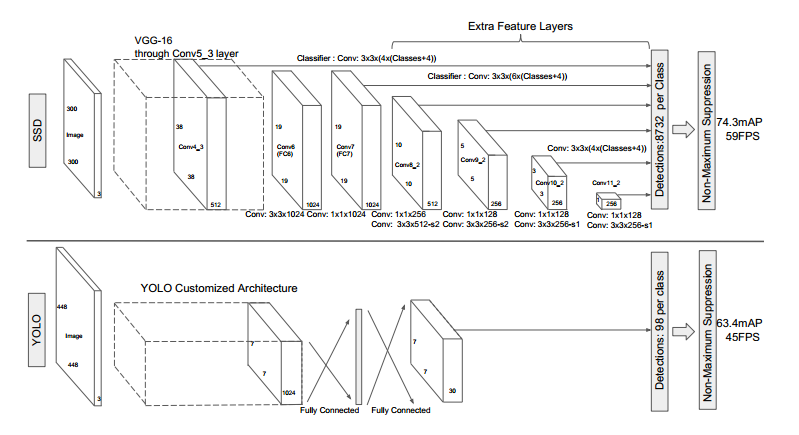
总结一下,网络模型的主要特征:
Multi-scale feature maps for detection
VGG中的 某些层以及VGG后面又添加的一些层中的某些层,被用来检测和分类。不同的feature layer 预测的bounding box的scale是不一样的,因此不同feature layer上的卷积模型也是不一样的(体现在参数和回归效果上)。
Convolutional predictors for detection
每一个被选中用于预测的feature layer,是用一个 3×3 的卷积层用于预测的,比如说某个feature layer的是 m×n×p 大小的,那么卷积核就是 3×3×p,这也是某一个 detector/classifier的参数量,它的输出是对应 bounding box中类别的得分或者相对于default box的坐标偏移量。对应于 feature map 上每个位置(cell),都会有 k 个 default box,那么无疑预测的时候要对每个位置上的每个default box都输出类别得分和坐标偏移。
Default boxes and aspect ratios
每一个被选中预测的feature layer ,其每个位置(cell)都关联k个default box,对每个default box都要输出C个类别得分和4个坐标偏移,因此每个default box有(C+4)个输出,每个位置有 (C+4)k 个输出,对于m×n 大小的feature map输出为 (C+4)kmn 个输出。
Training
匹配策略
检测=分类+定位,定位使用的是回归方法。
平面上任意两个不重合的框都是可以通过对其中一个框进行一定的变换(线性变换+对数变换)使二者重合。
在SSD中,通俗的说就是先产生一些预选的default box(类似于anchor box),然后标签是 ground truth box,预测的是bounding box,现在有三种框,从default box到ground truth有个变换关系,从default box到prediction bounding box有一个变换关系,如果这两个变换关系是相同的,那么就会导致 prediction bounding box 与 ground truth重合,如图:
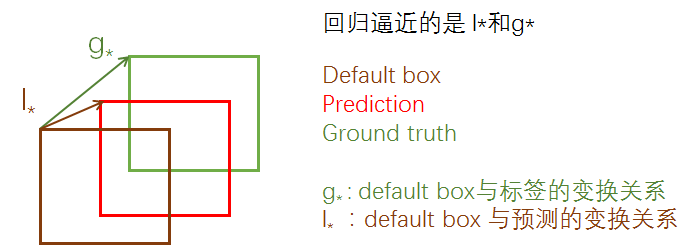
所以回归的就是这两个 变换关系: l∗与 g∗ ,只要二者接近,就可以使prediction bounding box接近 ground truth box 。上面的 g∗ 是只在训练的时候才有的,inference 时,就只有 l∗ 了,但是这时候的 l∗已经相当精确了,所以就可以产生比较准确的定位效果。
计算default box与任意的ground truth box之间的 杰卡德系数(jaccard overlap ),其实就是IOU,只要二者之间的阈值大于0.5,就认为这是个正样本。
训练目标
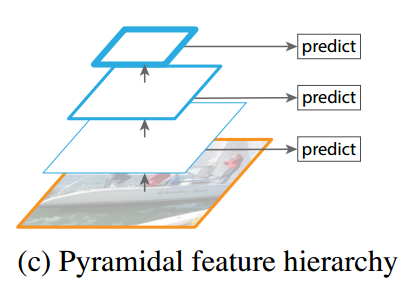
损失函数,包含了定位和分类:
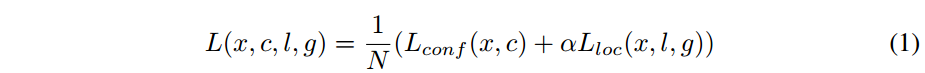
- N是匹配成功的正样本数量,如果N=0,则令 loss=0.
- α 是定位损失与分类损失之间的比重,这个值论文中提到是通过交叉验证的方式设置为 1 的。
定位损失,用的是smooth L1 loss
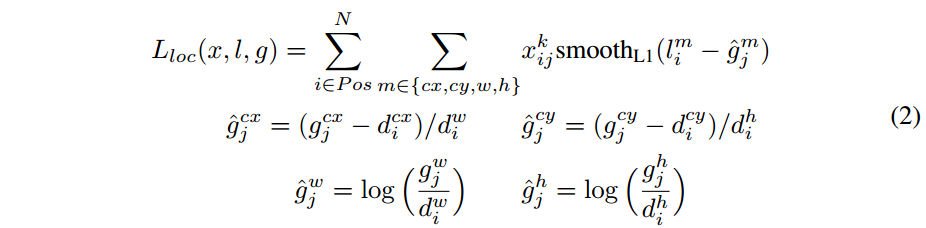
- l 代表预测bounding box与default box之间的变换关系, g 代表的是ground truth box与default box之间的变换关系。
- $x^p_ij$ 代表 第 i 个default box 与类别 p 的 第 j 个ground truth box 是否匹配,匹配为1,否则为0;
分类损失,softmax loss,交叉熵